Convergence of improper integrals examples. Convergence criteria for improper integrals of nonnegative functions. Comparison theorem for improper integrals

Theorem 12.11 (test for comparing improper integrals). Let the functions f (x) and g (x) be continuous on the interval [a, α\u003e) and satisfy the condition 0 fix)? (X) on it. Then from the convergence of the integral

it follows the convergence of the integral

and vice versa, the divergence of the integral (12.63) follows from the divergence of the integral (12.64).

Evidence. Let's introduce the notation:

Function P (K) is non-decreasing; indeed, if and Z 2, then

J fix) dx\u003e 0, and then

Let's take a sequence of values \u200b\u200b(/? „) -\u003e“\u003e; then the corresponding sequence of values \u200b\u200bof the function (F (R n)) is monotonic and non-decreasing. Let the integral (12.63) converge, then the sequence (67 ( R it)) is limited; but then the sequence is also limited (F (/? „)), And hence, by virtue of Theorem 7.13, it converges. Therefore, there is a limit F (R) at R - + «\u003e, i.e. integral (12.64) converges.

We now prove the second part of the theorem; let the integral (12.64) diverge. If we assume that the integral (12.63) converges, then by what was proved above the integral (12.64) must also converge, which contradicts the condition. The theorem is proved. ?

Comment. A similar comparison criterion is also valid for improper integrals of the second kind. If the functions f (x) and g (x) continuous on the half-interval [a\u003e b) and for all points in some neighborhood of the singular point b completed

conditions 0 (x), then the convergence of the integral Jg (x) dx implies the convergence

integral J / (x) dx, and from the divergence of the integral J / (x) dx,

integral Jg (x) dx.

Let us consider examples of investigating the convergence of improper integrals.

Example 27. T. ^ -.

X 3 (1 + e L)

Decision. Let us compare the integrand in this integral with the function

Dg. It is obvious that -r- -

x r * (1 + 0 x J

grain J-jdx converges; therefore, by virtue of the comparison criterion, the given x

integral.

Example 28. I-.

Decision. Comparing the integrand of this integral with the function 1 / x,

we see that (1 + In x) / x\u003e 1 / x on the interval 1

therefore, this integral diverges according to the comparison criterion.

In conclusion, we give, without proof, the Cauchy criterion for the convergence of an improper integral of the first kind.

12.10.4. Absolute and conditional convergence of improper integrals

Definition 5. An improper integral J / (x) dx is called absolutely

convergingif the integral J | / (x) | dx converges.

Definition 6. An improper integral J / (x) dx is called conditionally similar

dyingif it converges and the integral J | / (x) | dx diverges.

Note that the absolute convergence of the integral implies its convergence by virtue of estimate 3 of the definite integral and the Cauchy criterion.

Theorem 12.13 (Dirichlet - Abel test *). Let the function f (x) be continuous and have a bounded antiderivative F (x) on the interval [a, α\u003e), and the function g (x) has a continuous derivative on this interval, does not increase and tends to zero as x -\u003e © o. Then the improper integral

converges.

Evidence. We apply integration by parts to the integral J / (x) g (x) dx

on an arbitrary segment R R " from [ and, °°). We have:

Theorem 12.12. For the improper integral (12.64) to converge, it is necessary and sufficient that for any ε\u003e 0 one can find such a number AND \u003e 0, which for any R " and /? "greater than AND, inequality holds:

By the hypothesis of the theorem F (x) limited, i.e. | F (x) | K. The function g (x) does not increase and tends to zero as x - »«\u003e, hence. g (x) \u003e 0, a g "(x)

Abel Niels Henrik (1802-1829) - Norwegian mathematician.

Since, by the hypothesis of the theorem, g (x) - »0 as x -\u003e © °, for an arbitrary number e\u003e 0 one can find the number A\u003e such that for R "\u003e L the inequality g (R ") Substituting this into estimate (12.68), we obtain:

which corresponds to the Cauchy criterion for the convergence of the integral (12.66). The theorem is proved. ?

Let us consider examples of using the Dirichlet - Abel criterion for the convergence of improper integrals.

Example 29. f ^^ dx, a\u003e 0.

Decision. We put f (x) \u003d sin x, g (x) \u003d l / x "; it is easy to verify that all the conditions of the theorem are fulfilled, that is, this integral converges. For a\u003e 1, this integral

ral converges absolutely. Indeed, | sin x / xP 1 / dL, integral J (l / x e) dx

converges, i.e. by the comparison criterion (Theorem 12.11), the given integral also converges absolutely.

Example 30. Jsin х 2 dx - Fresnel integral, о

Decision. We represent this integral as a sum:

Since sin x 2 is a continuous function on the interval (0, 1J, the first integral in (12.69) exists. To clarify the convergence of the improper integral on the right-hand side of (12.69), we put f (x) \u003d x sin x 2, g (x) \u003d 1 / x. Then for the function f (x) the antiderivative F (x) = -cosx 2 /! is bounded on the interval | 1, «\u003e), and # (x) is positive, tends to zero as x -» oo and has a continuous derivative on (1, © o). Hence, according to the Dirichlet - Abel criterion, the second integral in (12.69) converges, i.e. the Fresnel integral also converges.

1. Improper integrals with infinite limits

Recall the definition of an integral as the limit of integral sums:

The definition assumes that the integration interval is finite, and the function f (x) is continuous in it. Violation of these assumptions leads to improper integrals.

Definition.If the integral tends to a finite limit with an unbounded increase "B", then this limit is called an improper integral with an infinite upper bound of the function f (x) and is denoted by the symbol

In this case, the improper integral is said to exist or converge.

If the specified limit does not exist or does exist, but is infinite, then they say that the integral does not exist or diverges.

An improper integral with an infinite lower bound is defined similarly:

An improper integral with two infinite boundaries is defined by the formula:

where c is any fixed point on the Ox axis.

So, improper integrals can be with an infinitely lower bound, with an infinitely upper bound, and also with two infinite boundaries.

Convergence criteria. Absolute and conditional convergence

The integral exists only if each of the integrals exists: and.

Example. Investigate the convergence of the integral

Assuming c \u003d 0, we get:

those. the integral converges.

Sometimes there is no need to calculate the improper integral, but it is enough just to know whether it converges or diverges by comparing it with another integral.

Comparison theorem for improper integrals.

Suppose that the function f (x) has several (finite number) discontinuity points of the first kind in the interval, this “obstacle” can be easily eliminated by dividing the segment by discontinuity points into several segments, calculating definite integrals on each separate segment and adding the results.

Consider a definite integral of a function that is unbounded when approaching one of the ends of a segment, for example, .

(In such cases, they usually say: '' The function has an infinite discontinuity at the right end of the integration segment ''.)

It is clear that the usual definition of an integral loses its meaning here.

Definition... By an improper integral of a function f (x) continuous for a £ x< b и неограниченной при x ® b - 0, называется предел:

The improper integral of a function with an infinite discontinuity at the left end of the segment is defined similarly:

Consequently, the integral diverges on the segment [-1, 0].

This means that the integral also diverges on the segment.

Thus, this integral diverges over the entire interval [-1, 1]. Note that if we began to calculate this integral, ignoring the discontinuity of the integrand at the point x \u003d 0, we would get an incorrect result. Really,

, which is impossible.

So, to study the improper integral of a discontinuous function, it is necessary to "split" it into several integrals and study them.

As you know, finding the integral can be a rather difficult task. It would be a great disappointment to start calculating the improper integral and find at the end of the path that it diverges. Therefore, of interest are methods that allow one to draw a conclusion about the convergence or divergence of an improper integral without serious calculations for one type of functions. The first and second comparison theorems, which will be considered below, largely help to investigate improper convergence integrals.

Let f (x)? 0. Then the functions

are monotonically increasing in the variables t or -d (since we take q\u003e 0, -d tends to zero from the left). If with increasing arguments the functions F 1 (t) and F 2 (-e) remain bounded above, this means that the corresponding improper integrals converge. This is the basis of the first comparison theorem for integrals of non-negative functions.

Let the following conditions be satisfied for the function f (x) and g (x) at x? A:

• 1) 0? F (x)? G (x);
• 2) The functions f (x) and g (x) are continuous.

Then the convergence of the integral implies the convergence of the integral, and the divergence of the integral implies the divergence

Since 0? F (x)? G (x) and the functions are continuous, then

By hypothesis, the integral converges, i.e. has a finite value. Hence, the integral converges as well.

Now let the integral diverge. Suppose the integral converges, but then the integral must converge, which contradicts the condition. Our assumption is wrong, the integral diverges.

Comparison theorem for improper integrals of the second kind.

Let, for the functions f (x) and g (x) on the interval, increase unboundedly for x\u003e +0. For it, for x\u003e +0, the inequality<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

Comparison theorem for improper integrals of the first kind.

Let for the function f (x) and g (x) be on the interval, and the interval of integration is finite, that is, it is bounded by numbers, not infinity. Some tasks lead to the need to abandon these restrictions. This is how improper integrals appear.

Geometric meaning of improper integral it turns out quite simply. In the case when the graph of the function y = f(x) is above the axis Ox , the definite integral expresses the area of \u200b\u200ba curved trapezoid bounded by the curve y = f(x) , abscissa and ordinates x = a , x = b ... In turn, the improper integral expresses the area of \u200b\u200ban unbounded (infinite) curvilinear trapezoid enclosed between the lines y = f(x) (in the picture below - red), x = a and the abscissa.

Improper integrals are defined in a similar way for other infinite intervals:

The area of \u200b\u200ban infinite curvilinear trapezoid can be a finite number, and in this case the improper integral is called convergent. The area can be infinite, and in this case the improper integral is called divergent.

Using the limit of the integral instead of the improper integral itself. In order to calculate the improper integral, one must use the limit of the definite integral. If this limit exists and is finite (not equal to infinity), then the improper integral is called convergent, and otherwise, divergent. What the variable tends to under the limit sign depends on whether we are dealing with an improper integral of the first kind or of the second kind. We'll find out about it now.

Improper integrals of the first kind - with infinite limits and their convergence

Improper integrals with infinite upper limit

So, the representation of an improper integral differs from the usual definite integral in that the upper limit of integration is infinite.

Definition. Improper integral with infinite upper limit of integration of a continuous function f(x) between a before ∞ is the limit of the integral of this function with the upper limit of integration b and the lower limit of integration a provided that the upper limit of integration grows indefinitely, i.e.

.

If this limit exists and is equal to some number, not infinity, then an improper integral is called convergent, and the number that the limit is equal to is taken as its value. Otherwise an improper integral is called divergent and no significance is attributed to it.

Example 1. Calculate the improper integral (if it converges).

Decision. Based on the definition of the improper integral, we find

Since the limit exists and is equal to 1, then this the improper integral converges and is equal to 1.

In the next example, the integrand is almost the same as in example 1, only the degree of x is not two, but the letter alpha, and the problem is to study the improper integral for convergence. That is, the question remains to be answered: at what values \u200b\u200bof alpha does this improper integral converge, and at which values \u200b\u200bdoes it diverge?

Example 2. Investigate the improper integral (the lower limit of integration is greater than zero).

Decision. Suppose first that, then

In the resulting expression, we pass to the limit at:

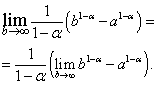
It is easy to see that the limit on the right side exists and is zero when, that is, and does not exist, when, that is.

In the first case, that is, at takes place. If, then and does not exist.

The conclusion of our study is as follows: given the improper integral converges at and diverges at.

Applying to the studied form of the improper integral the Newton-Leibniz formula , you can derive the following formula, which is very similar to it:

.

This is the generalized Newton-Leibniz formula.

Example 3. Calculate the improper integral (if it converges).

The limit of this integral exists:

The second integral is the sum that expresses the original integral:

The limit of this integral also exists:

.

We find the sum of two integrals, which is also the value of the original improper integral with two infinite limits:

Improper integrals of the second kind - of unbounded functions and their convergence

Let the function f(x) given on the segment from a before b and unlimited on it. Suppose that the function goes to infinity at the point b , while at all other points of the segment it is continuous.

Definition. Improper integral of the function f(x) on the segment from a before b is the limit of the integral of this function with the upper limit of integration c if, while striving c to b the function increases indefinitely, and at the point x = b function is not defined, i.e.

.

If this limit exists, then the improper integral of the second kind is called converging, otherwise, divergent.

Using the Newton-Leibniz formula, we derive.

Examples of investigating improper integrals for convergence

Example 1
.

Thus, this integral converges for a\u003e 1 and diverges for a £ 1.

Example 2 Investigate for convergence. We calculate the integral by definition:
.

Thus, this integral converges for a<1 и расходится при a³1.

Example 3 Investigate for convergence .

<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два

.

We investigate the convergence of the first integral I1 using an equivalent function: (since n\u003e 0), and the integral converges for m\u003e -1 (example 2). Similarly, for the integral I2:

And the integral converges for m + n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 and m + n<-1, и будет расходится при нарушении хотя бы одного из них.

Example 4 Investigate for convergence.

The integrand can be infinitely large (if m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:

Since arctgx »x for x®0, the integral I1 is equivalent to an integral that converges for m + 1\u003e -1, ie, for m\u003e -2 (example 1).

For the integrand in the improper integral of the first kind I2, we choose an equivalent:

since arctgx »p / 2 for x® ¥. Therefore, according to the second comparison criterion, the integral I2 will converge for m + n<-1, и расходится в противном случае.

Combining the conditions for the convergence of the integrals I1 and I2, we obtain the conditions for the convergence of the original integral: m\u003e -2 and m + n<-1 одновременно.

Comment. In examples 2-4, 2 comparison criteria were used, which provides necessary and sufficient conditions for convergence, which allows, having established convergence under a certain condition on the values \u200b\u200bof the parameters, not to prove the divergence of the integral if the obtained convergence conditions are violated.

Example 5 Investigate for convergence.

This integral contains a singular point 0, at which the integrand can go to infinity for p<0, поэтому снова разобьем исходный интеграл на два:

.

The integral I1 is an improper integral of the second kind, and the integrand is equivalent for x®0 to the function xp (e-x ®1 for x®0), that is, I1 converges for p\u003e -1 (Example 1).

The integral I2 is an improper integral of the first kind. It is not possible to find a function equivalent to the integrand so that it does not contain an exponential function. Therefore, you cannot use comparison feature 2, as in the previous examples. Let us apply the first comparison criterion, for which we use the following known fact:

For a\u003e 0 and any p. From this, and the fact that the function xpe-ax is continuous, it follows that this function is bounded, that is, there exists a constant M\u003e 0 such that xpe-ax< M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:

That is, the integral I2 converges for any p.

Thus, the original integral converges for p\u003e -1.

Example 6 Investigate for convergence.

Let's change the variable: t \u003d lnx, and get

The partition of the integral into two is performed similarly to Example 5. The integral I1 is completely equivalent to the integral I1 from Example 5 and, therefore, converges for q<1.

Consider the integral I2. Provided 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения and a \u003d (1-p) / 2.).

So, I2 converges for p\u003e 1. However, this is not the end of the study of the convergence of this integral, since the used convergence criterion gives only sufficient conditions for convergence. Therefore, it is necessary to study the convergence for 1-p £ 0.

Consider the case p \u003d 1. Then the integral I2 is equivalent, which converges for q\u003e 1 (note that in this case the integral I1 diverges) and diverges otherwise.

For p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что For 1-p\u003e 0, and, therefore, starting from some A\u003e 1, T- QE(1- P) T ³ M \u003d const\u003e 0. Then the integral I2 satisfies the estimate

,

Where the integral on the right-hand side diverges, which proves the divergence of the integral I2.

Summarizing the results obtained, we find that the original integral converges for q<1 и p>1, otherwise the integral diverges.

Example 6 Investigate for absolute and conditional convergence.

We split the original integral into two:

.

Convergence. The integral I1 is equivalent to , i.e., converges for p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.

The integral I2 converges about the Dirichlet-Abel criterion for p\u003e 0 because the antiderivative sin (x) is bounded, and the function 1 / xp tends to zero monotonically as x tends to infinity.

Let us show that the integral diverges for p £ 0. For this we use the Cauchy criterion, or rather, its negation

.

We take the following quantities as R1 and R2: R1 \u003d 2pk and R2 \u003d 2pk + p / 2, then

, for p\u003e 0.

Thus, the integral converges at 0

Absolute convergence The absolute convergence of the integral I1 has already been established; consider the absolute convergence of I2. Let us estimate the integral from above:

, i.e., the integral converges for p\u003e 1.

To prove the divergence for p £ 1, we estimate the integral from below

.

We split the last integral of the difference of functions into the difference of integrals

.

If both integrals converge, then the integral of the difference also converges, if one of the integrals diverges and the other converges, then the integral of the difference diverges. In the case of divergence of both integrals, the convergence of the integral of the difference is subject to further study. We are interested in the second of the described cases.

Diverges (example 1) at p<1. сходится по признаку Дирихле-Абеля при 1>p\u003e 0 (see Convergence), hence the integral is estimated from below by a diverging integral, i.e., diverges.

We are not interested in the case p³1, since the integral diverges for these values \u200b\u200bof the parameter.

Thus, the original integral converges absolutely at 0