All about religion and faith - “prayer to Saint Paraskeva for peace in the family” with detailed...


Lesson topic: "Decimal fractions and operations with them."
Lesson objectives: to repeat and systematize students’ knowledge and skills on the topic “decimal fractions”, to determine the level of knowledge acquisition on this topic, to check the degree of mastery of the material; develop attention, memory, speech, logical thinking, independence; cultivate the desire to achieve goals, a sense of responsibility, self-confidence, and the ability to work in a team.
Lesson objectives: Show the importance of practicing computational skills at this stage of training. Stimulate students' motivation to study mathematics;
Lesson type: lesson on generalization, systematization and correction of knowledge and skills on the topic: “Decimal fractions”
Forms of student work: frontal, group, individual
Equipment: laptop, presentation, test on the topic “All actions with decimals”, task cards, a set of signal cards for each student (red, green, yellow).
During the classes
Organizing time.
Hello guys!
Please take your seats.
Today is February 13th,
Day of the week – Friday
Today we will spend
The lesson is this
which will be dedicated
One interesting person.
Listen to me carefully
Answer the questions
That's it, guys, take note.
Don't forget anything
Please don't let me down.
Come on, my young friend,
Are you ready to start the lesson?
Is everything okay on the table?
Is there order in your head?
To have knowledge
It will take patience and effort.
Lesson motivation.
We studied fractions for a long time,
Compare, round,
Added, subtracted,
Multiplied and divided
The arithmetic mean was found.
And now the time has come
To check everything for you.
How do you solve problems?
Multiply the fraction by ten
How do you solve equations?
Do you know many examples?
We will check everything with you
And at the end we give an order:
Or give you an A, or teach you to send you away!
And to cope successfully we must:
Answer questions asked clearly and concisely;
Quickly and correctly calculate proposed tasks;
Provide assistance in work;
Be able to listen to others, etc.
Lesson motto: Have excellent knowledge on the topic “Decimal Fractions!”
3. Historical background slide 3-5
4. Updating basic knowledge
a) Game “Chamomile”. The goal of the game is to repeat the rules that will be required when solving problems.
(A chamomile flower is attached to the board using a magnet, with questions written on each petal. Opening the petal, the student answers the question posed):
Rules for adding and subtracting decimals
Rules for multiplying decimal fractions by 10, 100, 1000:.
Rules for dividing decimal fractions by 10, 100, 1000:.
Rules for multiplying decimals by natural number
Rules for multiplying decimals by decimals
Rules for dividing decimal fractions by natural numbers
Rules for dividing decimals by decimals
Rules for comparing decimal fractions
b). And now oral calculation will be useful to us.
“Health is not everything, but everything without health is nothing.” Socrates
5. Consolidation of acquired knowledge. Work in notebooks.
Assignment for students.
1. Mathematical dictation
Students write down only their answers on pieces of paper.
1) 24,04: 2= 12,02
2) 1.3 1.5 + 1.5 1.7 = 4.5
3) 8,07 + 4,1 = 12,17
4) 1,28 +3,4 +1,72 -2,4 = 4
6) 0.7 · * =0.007 (instead of * put a number to get the correct equality) 0.01
7) 7.8 · 3.5 – 7.8 · 3.4 =0.78
8) 2,54: * = 2540 = 0,001
9) 9,6: 100 =0,096
2). Right answers:
| 1) 12.02 W 4) 4 I 7) 0.78 P |
| 2) 4.5 K 5) 40 A 8) 0.001 C |
| 3) 12.17 U 6) 0.01. 9) 0.096 N |
Students exchange papers and give marks
Arrange the letters in the table according to the answers.
2) The clown came up with several examples of adding, subtracting and multiplying decimal fractions, and to make it funnier, he erased the commas in them. Here are the equalities he came up with:
34 * 0,01 = 0034
Putting commas in the right place
3) Solve problems:
1. On Monday, 37.6 tons of grain were threshed, on Tuesday - 3.8 tons more than on Monday, and on Wednesday - 1.5 times less than on Tuesday. How many tons of grain were threshed in these three days?
2. The tourists walked to the river at a speed of 6.6 km/h, and along the river bank at a speed of 4.2 km/h. In total they walked 9.06 km. How long did the tourists walk along the shore if they walked 0.8 hours to the river?
6. Physical education minute
In class we wrote,
They answered everything they knew.
Now we'll rest
And let's start writing again!
Having relieved the tension that had accumulated while solving the problem and equations, let’s continue working in the notebook.
7. Test on the topic “Addition, subtraction, multiplication, division of decimals”
Now let's test our knowledge with a test.
Option 1
1) Perform addition:
2) Do the multiplication:
3) Find the value of the quotient:
Additionally:
Find the meaning of the expression:
4,36: (3,15 + 2,3)
Option 2
1) Perform addition:
2) Do the multiplication:
3) Find the value of the quotient:
Additionally:
Find the meaning of the expression:
6,93: (0,028 + 1,512)
Key to the test:
1) 2) 3) Add.
I. option B) A) B) C)
II. option A) B) C) C)
We check the work ourselves. Next to each task we put a “+” or “–” sign.
Let's evaluate the result
Criteria for evaluation:
“5” – 5 tasks; “4” – 4 tasks; “3” – 3 tasks.
Show with the help of a signal card which score you received: “5” – red, “4” – green, “3” – yellow.
8. Work in pairs
Follow the steps. Cross out the answers and the letters corresponding to them in the table. The remaining letters will allow you to read the word.
1) 5,8 + 22,191=
2) 6.025 x 5.6 =
3) 1.15 x 0.4 =
5) 131,67: 5,7 =
1,4 23,1 0,46 2,11 0,14 0,4 27,991 3,4 33,74 27 8,22 2,6
M P Y O Z L O V D E C
Answer: the word WELL DONE
9. Homework:
Well done to all of you!
You are all daredevils!
And let my beloved for years
Math will always be there for you!
Repeat steps 22-37. Solve tasks No. 1317, 1321, 1333
Come up with and beautifully draw up a problem on a landscape sheet that could be solved using addition and subtraction of decimal fractions, write down the condition of the problem on a piece of paper and draw a picture based on this condition, and write down its solution in a notebook. Try to ensure that the students in the class like your task so that the data in the condition corresponds to reality.
10. Lesson summary. Reflection. Microphone principle. (Students take turns giving a reasoned answer to one of the questions).
I enjoyed my lesson today...
Today in class I repeated...
Today in class I reinforced...
Today in class I graded myself...
What types of work caused difficulties and require repetition...
What knowledge are you confident in...
Did the lesson help you advance in your knowledge, skills, and abilities in the subject...
Who needs more work, on what...
How effective was the lesson today...

In this tutorial we will look at each of these operations separately.
Lesson contentAs we know, a decimal fraction consists of an integer and a fractional part. When adding decimals, the whole and fractional parts are added separately.
For example, let's add the decimal fractions 3.2 and 5.3. It is more convenient to add decimal fractions in a column.
Let us first write these two fractions in a column, with the integer parts necessarily being under the integers, and the fractional parts under the fractional ones. At school this requirement is called "comma under comma" .
Let's write the fractions in a column so that the comma is under the comma:
We add the fractional parts: 2 + 3 = 5. We write the five in the fractional part of our answer:
Now we add up the whole parts: 3 + 5 = 8. We write an eight in the whole part of our answer:
Now we separate the whole part from the fractional part with a comma. To do this, we again follow the rule "comma under comma" :
We received an answer of 8.5. This means that the expression 3.2 + 5.3 equals 8.5
3,2 + 5,3 = 8,5
In fact, not everything is as simple as it seems at first glance. There are also pitfalls here, which we will talk about now.
Decimal fractions, like ordinary numbers, have their own digits. These are places of tenths, places of hundredths, places of thousandths. In this case, the digits begin after the decimal point.
The first digit after the decimal point is responsible for the tenths place, the second digit after the decimal point for the hundredths place, and the third digit after the decimal point for the thousandths place.
Places in decimal fractions contain some useful information. Specifically, they tell you how many tenths, hundredths, and thousandths there are in a decimal.
For example, consider the decimal fraction 0.345
The position where the three is located is called tenth place
The position where the four is located is called hundredths place
The position where the five is located is called thousandth place

Let's look at this drawing. We see that there is a three in the tenths place. This means that there are three tenths in the decimal fraction 0.345.
If we add the fractions, we get the original decimal fraction 0.345

At first we got the answer, but we converted it to a decimal fraction and got 0.345.
When adding decimal fractions, the same rules apply as when adding ordinary numbers. The addition of decimal fractions occurs in digits: tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.
Therefore, when adding decimal fractions, you must follow the rule "comma under comma". The comma under the comma provides the very order in which tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.
Example 1. Find the value of the expression 1.5 + 3.4
First of all, we add up the fractional parts 5 + 4 = 9. We write nine in the fractional part of our answer:
Now we add the integer parts 1 + 3 = 4. We write the four in the integer part of our answer:
Now we separate the whole part from the fractional part with a comma. To do this, we again follow the “comma under comma” rule:
We received an answer of 4.9. This means that the value of the expression 1.5 + 3.4 is 4.9
Example 2. Find the value of the expression: 3.51 + 1.22
We write this expression in a column, observing the “comma under comma” rule.
First of all, we add up the fractional part, namely the hundredths of 1+2=3. We write a triple in the hundredth part of our answer:
Now add the tenths 5+2=7. We write a seven in the tenth part of our answer:
Now we add the whole parts 3+1=4. We write the four in the whole part of our answer:
We separate the whole part from the fractional part with a comma, observing the “comma under comma” rule:
The answer we received was 4.73. This means the value of the expression 3.51 + 1.22 is equal to 4.73
3,51 + 1,22 = 4,73
As with regular numbers, when adding decimals, . In this case, one digit is written in the answer, and the rest are transferred to the next digit.
Example 3. Find the value of the expression 2.65 + 3.27
We write this expression in the column:
Add the hundredths parts 5+7=12. The number 12 will not fit into the hundredth part of our answer. Therefore, in the hundredth part we write the number 2, and move the unit to the next digit:
Now we add the tenths of 6+2=8 plus the unit that we got from the previous operation, we get 9. We write the number 9 in the tenth of our answer:
Now we add the whole parts 2+3=5. We write the number 5 in the integer part of our answer:
The answer we received was 5.92. This means the value of the expression 2.65 + 3.27 is equal to 5.92
2,65 + 3,27 = 5,92
Example 4. Find the value of the expression 9.5 + 2.8
We write this expression in the column
We add the fractional parts 5 + 8 = 13. The number 13 will not fit into the fractional part of our answer, so we first write down the number 3, and move the unit to the next digit, or rather, transfer it to the integer part:
Now we add the integer parts 9+2=11 plus the unit that we got from the previous operation, we get 12. We write the number 12 in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
We received the answer 12.3. This means that the value of the expression 9.5 + 2.8 is 12.3
9,5 + 2,8 = 12,3
When adding decimals, the number of digits after the decimal point in both fractions must be the same. If there are not enough numbers, then these places in the fractional part are filled with zeros.
Example 5. Find the value of the expression: 12.725 + 1.7
Before writing this expression in a column, let’s make the number of digits after the decimal point in both fractions the same. The decimal fraction 12.725 has three digits after the decimal point, but the fraction 1.7 has only one. This means that in the fraction 1.7 you need to add two zeros at the end. Then we get the fraction 1.700. Now you can write this expression in a column and start calculating:

Add the thousandths parts 5+0=5. We write the number 5 in the thousandth part of our answer:

Add the hundredths parts 2+0=2. We write the number 2 in the hundredth part of our answer:

Add the tenths 7+7=14. The number 14 will not fit into a tenth of our answer. Therefore, we first write down the number 4, and move the unit to the next digit:

Now we add the integer parts 12+1=13 plus the unit that we got from the previous operation, we get 14. We write the number 14 in the integer part of our answer:

Separate the whole part from the fractional part with a comma:

We received a response of 14,425. This means the value of the expression 12.725+1.700 is 14.425
12,725+ 1,700 = 14,425
When subtracting decimal fractions, you must follow the same rules as when adding: “comma under the decimal point” and “equal number of digits after the decimal point.”
Example 1. Find the value of the expression 2.5 − 2.2
We write this expression in a column, observing the “comma under comma” rule:
We calculate the fractional part 5−2=3. We write the number 3 in the tenth part of our answer:
We calculate the integer part 2−2=0. We write zero in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
We received an answer of 0.3. This means the value of the expression 2.5 − 2.2 is equal to 0.3
2,5 − 2,2 = 0,3
Example 2. Find the value of the expression 7.353 - 3.1
This expression has a different number of decimal places. The fraction 7.353 has three digits after the decimal point, but the fraction 3.1 has only one. This means that in the fraction 3.1 you need to add two zeros at the end to make the number of digits in both fractions the same. Then we get 3,100.
Now you can write this expression in a column and calculate it:

We received a response of 4,253. This means the value of the expression 7.353 − 3.1 is equal to 4.253
7,353 — 3,1 = 4,253
As with ordinary numbers, sometimes you will have to borrow one from an adjacent digit if subtraction becomes impossible.
Example 3. Find the value of the expression 3.46 − 2.39
Subtract hundredths of 6−9. You cannot subtract the number 9 from the number 6. Therefore, you need to borrow one from the adjacent digit. By borrowing one from the adjacent digit, the number 6 turns into the number 16. Now you can calculate the hundredths of 16−9=7. We write a seven in the hundredth part of our answer:
Now we subtract tenths. Since we took one unit in the tenths place, the figure that was located there decreased by one unit. In other words, in the tenths place there is now not the number 4, but the number 3. Let's calculate the tenths of 3−3=0. We write zero in the tenth part of our answer:
Now we subtract the whole parts 3−2=1. We write one in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
We received an answer of 1.07. This means the value of the expression 3.46−2.39 is equal to 1.07
3,46−2,39=1,07
Example 4. Find the value of the expression 3−1.2
This example subtracts a decimal from a whole number. Let's write this expression in a column so that the whole part of the decimal fraction 1.23 is under the number 3
Now let's make the number of digits after the decimal point the same. To do this, after the number 3 we put a comma and add one zero:
Now we subtract tenths: 0−2. You cannot subtract the number 2 from zero. Therefore, you need to borrow one from the adjacent digit. Having borrowed one from the neighboring digit, 0 turns into the number 10. Now you can calculate the tenths of 10−2=8. We write an eight in the tenth part of our answer:
Now we subtract the whole parts. Previously, the number 3 was located in the whole, but we took one unit from it. As a result, it turned into the number 2. Therefore, from 2 we subtract 1. 2−1=1. We write one in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
The answer we received was 1.8. This means the value of the expression 3−1.2 is 1.8
Multiplying decimals is simple and even fun. To multiply decimals, you multiply them like regular numbers, ignoring the commas.
Having received the answer, you need to separate the whole part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in both fractions, then count the same number of digits from the right in the answer and put a comma.
Example 1. Find the value of the expression 2.5 × 1.5
Let's multiply these decimal fractions like ordinary numbers, ignoring the commas. To ignore the commas, you can temporarily imagine that they are absent altogether:

We got 375. In this number, you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fractions 2.5 and 1.5. The first fraction has one digit after the decimal point, and the second fraction also has one. Total two numbers.
We return to the number 375 and begin to move from right to left. We need to count two digits to the right and put a comma:

We received an answer of 3.75. So the value of the expression 2.5 × 1.5 is 3.75
2.5 × 1.5 = 3.75
Example 2. Find the value of the expression 12.85 × 2.7
Let's multiply these decimal fractions, ignoring the commas:

We got 34695. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fractions 12.85 and 2.7. The fraction 12.85 has two digits after the decimal point, and the fraction 2.7 has one digit - a total of three digits.
We return to the number 34695 and begin to move from right to left. We need to count three digits from the right and put a comma:

We received a response of 34,695. So the value of the expression 12.85 × 2.7 is 34.695
12.85 × 2.7 = 34.695
Sometimes situations arise when you need to multiply a decimal fraction by a regular number.
To multiply a decimal and a number, you multiply them without paying attention to the comma in the decimal. Having received the answer, you need to separate the whole part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the decimal fraction, then count the same number of digits from the right in the answer and put a comma.
For example, multiply 2.54 by 2
Multiply the decimal fraction 2.54 by the usual number 2, ignoring the comma:

We got the number 508. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.54. The fraction 2.54 has two digits after the decimal point.
We return to number 508 and begin to move from right to left. We need to count two digits to the right and put a comma:

We received an answer of 5.08. So the value of the expression 2.54 × 2 is 5.08
2.54 × 2 = 5.08
Multiplying decimals by 10, 100, or 1000 is done in the same way as multiplying decimals by regular numbers. You need to perform the multiplication, not paying attention to the comma in the decimal fraction, then in the answer, separate the whole part from the fractional part, counting from the right the same number of digits as there were digits after the decimal point.
For example, multiply 2.88 by 10
Multiply the decimal fraction 2.88 by 10, ignoring the comma in the decimal fraction:

We got 2880. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.88. We see that the fraction 2.88 has two digits after the decimal point.
We return to the number 2880 and begin to move from right to left. We need to count two digits to the right and put a comma:

We received an answer of 28.80. Let's drop the last zero and get 28.8. This means that the value of the expression 2.88×10 is 28.8
2.88 × 10 = 28.8
There is a second way to multiply decimal fractions by 10, 100, 1000. This method is much simpler and more convenient. It consists in moving the decimal point to the right by as many digits as there are zeros in the factor.
For example, let's solve the previous example 2.88×10 this way. Without giving any calculations, we immediately look at the factor 10. We are interested in how many zeros there are in it. We see that there is one zero in it. Now in the fraction 2.88 we move the decimal point to the right one digit, we get 28.8.
2.88 × 10 = 28.8
Let's try to multiply 2.88 by 100. We immediately look at the factor 100. We are interested in how many zeros there are in it. We see that there are two zeros in it. Now in the fraction 2.88 we move the decimal point to the right two digits, we get 288
2.88 × 100 = 288
Let's try to multiply 2.88 by 1000. We immediately look at the factor 1000. We are interested in how many zeros there are in it. We see that there are three zeros in it. Now in the fraction 2.88 we move the decimal point to the right by three digits. There is no third digit there, so we add another zero. As a result, we get 2880.
2.88 × 1000 = 2880
Multiplying decimals by 0.1, 0.01, and 0.001 works in the same way as multiplying a decimal by a decimal. It is necessary to multiply the fractions like ordinary numbers, and put a comma in the answer, counting as many digits to the right as there are digits after the decimal point in both fractions.
For example, multiply 3.25 by 0.1
We multiply these fractions like ordinary numbers, ignoring the commas:

We got 325. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fractions 3.25 and 0.1. The fraction 3.25 has two digits after the decimal point, and the fraction 0.1 has one digit. Total three numbers.
We return to the number 325 and begin to move from right to left. We need to count three digits from the right and put a comma. After counting down three digits, we find that the numbers have run out. In this case, you need to add one zero and add a comma:

We received an answer of 0.325. This means that the value of the expression 3.25 × 0.1 is 0.325
3.25 × 0.1 = 0.325
There is a second way to multiply decimals by 0.1, 0.01 and 0.001. This method is much simpler and more convenient. It consists in moving the decimal point to the left by as many digits as there are zeros in the factor.
For example, let's solve the previous example 3.25 × 0.1 this way. Without giving any calculations, we immediately look at the multiplier of 0.1. We are interested in how many zeros there are in it. We see that there is one zero in it. Now in the fraction 3.25 we move the decimal point to the left by one digit. By moving the comma one digit to the left, we see that there are no more digits before the three. In this case, add one zero and put a comma. The result is 0.325
3.25 × 0.1 = 0.325
Let's try multiplying 3.25 by 0.01. We immediately look at the multiplier of 0.01. We are interested in how many zeros there are in it. We see that there are two zeros in it. Now in the fraction 3.25 we move the decimal point to the left two digits, we get 0.0325
3.25 × 0.01 = 0.0325
Let's try multiplying 3.25 by 0.001. We immediately look at the multiplier of 0.001. We are interested in how many zeros there are in it. We see that there are three zeros in it. Now in the fraction 3.25 we move the decimal point to the left by three digits, we get 0.00325
3.25 × 0.001 = 0.00325
Do not confuse multiplying decimal fractions by 0.1, 0.001 and 0.001 with multiplying by 10, 100, 1000. A typical mistake for most people.
When multiplying by 10, 100, 1000, the decimal point is moved to the right by the same number of digits as there are zeros in the multiplier.
And when multiplying by 0.1, 0.01 and 0.001, the decimal point is moved to the left by the same number of digits as there are zeros in the multiplier.
If at first it is difficult to remember, you can use the first method, in which multiplication is performed as with ordinary numbers. In the answer, you will need to separate the whole part from the fractional part, counting the same number of digits on the right as there are digits after the decimal point in both fractions.
In one of the previous lessons, we said that when dividing a smaller number by a larger number, a fraction is obtained, the numerator of which is the dividend, and the denominator is the divisor.
For example, to divide one apple between two, you need to write 1 (one apple) in the numerator, and write 2 (two friends) in the denominator. As a result, we get the fraction . This means each friend will get an apple. In other words, half an apple. The fraction is the answer to the problem “how to divide one apple into two”

It turns out that you can solve this problem further if you divide 1 by 2. After all, the fractional line in any fraction means division, and therefore this division is allowed in the fraction. But how? We are accustomed to the fact that the dividend is always greater than the divisor. But here, on the contrary, the dividend is less than the divisor.
Everything will become clear if we remember that a fraction means crushing, division, division. This means that the unit can be split into as many parts as desired, and not just into two parts.
When you divide a smaller number by a larger number, you get a decimal fraction in which the integer part is 0 (zero). The fractional part can be anything.
So, let's divide 1 by 2. Let's solve this example with a corner:
One cannot be completely divided into two. If you ask a question “how many twos are there in one” , then the answer will be 0. Therefore, in the quotient we write 0 and put a comma:
Now, as usual, we multiply the quotient by the divisor to get the remainder:
The moment has come when the unit can be split into two parts. To do this, add another zero to the right of the resulting one:
We got 10. Divide 10 by 2, we get 5. We write the five in the fractional part of our answer:
Now we take out the last remainder to complete the calculation. Multiply 5 by 2 to get 10
We received an answer of 0.5. So the fraction is 0.5
Half an apple can also be written using the decimal fraction 0.5. If we add these two halves (0.5 and 0.5), we again get the original one whole apple: 

This point can also be understood if you imagine how 1 cm is divided into two parts. If you divide 1 centimeter into 2 parts, you get 0.5 cm

Example 2. Find the value of the expression 4:5
How many fives are there in a four? Not at all. We write 0 in the quotient and put a comma:
We multiply 0 by 5, we get 0. We write a zero under the four. Immediately subtract this zero from the dividend:
Now let's start splitting (dividing) the four into 5 parts. To do this, add a zero to the right of 4 and divide 40 by 5, we get 8. We write eight in the quotient.

We complete the example by multiplying 8 by 5 to get 40:

We received an answer of 0.8. This means the value of the expression 4:5 is 0.8
Example 3. Find the value of expression 5: 125
How many numbers are 125 in five? Not at all. We write 0 in the quotient and put a comma:

We multiply 0 by 5, we get 0. We write 0 under the five. Immediately subtract 0 from five

Now let's start splitting (dividing) the five into 125 parts. To do this, we write a zero to the right of this five:

Divide 50 by 125. How many numbers are 125 in the number 50? Not at all. So in the quotient we write 0 again

Multiply 0 by 125, we get 0. Write this zero under 50. Immediately subtract 0 from 50
Now divide the number 50 into 125 parts. To do this, we write another zero to the right of 50:
Divide 500 by 125. How many numbers are 125 in the number 500? There are four numbers 125 in the number 500. Write the four in the quotient:

We complete the example by multiplying 4 by 125 to get 500

We received an answer of 0.04. This means the value of expression 5: 125 is 0.04
So, let’s put a comma after the unit in the quotient, thereby indicating that the division of integer parts is over and we are proceeding to the fractional part:
Let's add zero to the remainder 4
Now divide 40 by 5, we get 8. We write eight in the quotient:
40−40=0. We got 0 left. This means that the division is completely completed. Dividing 9 by 5 gives the decimal fraction 1.8:
9: 5 = 1,8
Example 2. Divide 84 by 5 without a remainder
First, divide 84 by 5 as usual with a remainder:

We got 16 in private and 4 more left. Now let's divide this remainder by 5. Put a comma in the quotient, and add 0 to the remainder 4

Now we divide 40 by 5, we get 8. We write the eight in the quotient after the decimal point:

and complete the example by checking whether there is still a remainder:

A decimal fraction, as we know, consists of an integer and a fractional part. When dividing a decimal fraction by a regular number, you first need to:
For example, divide 4.8 by 2
Let's write this example in a corner:

Now let's divide the whole part by 2. Four divided by two equals two. We write two in the quotient and immediately put a comma:

Now we multiply the quotient by the divisor and see if there is a remainder from the division:

4−4=0. The remainder is zero. We do not write down zero yet, since the solution is not completed. Next, we continue to calculate as in ordinary division. Take down 8 and divide it by 2

8: 2 = 4. We write the four in the quotient and immediately multiply it by the divisor:

We received an answer of 2.4. The value of the expression 4.8:2 is 2.4
Example 2. Find the value of the expression 8.43: 3

Divide 8 by 3, we get 2. Immediately put a comma after the 2:

Now we multiply the quotient by the divisor 2 × 3 = 6. We write the six under the eight and find the remainder:

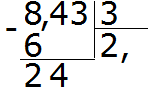
Divide 24 by 3, we get 8. We write eight in the quotient. Immediately multiply it by the divisor to find the remainder of the division:

24−24=0. The remainder is zero. We don’t write down zero yet. We take away the last three from the dividend and divide by 3, we get 1. Immediately multiply 1 by 3 to complete this example:

The answer we received was 2.81. This means the value of the expression 8.43: 3 is 2.81
To divide a decimal fraction by a decimal fraction, you need to move the decimal point in the dividend and divisor to the right by the same number of digits as there are after the decimal point in the divisor, and then divide by the usual number.
For example, divide 5.95 by 1.7
Let's write this expression with a corner

Now in the dividend and in the divisor we move the decimal point to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. This means that in the dividend and divisor we must move the decimal point to the right by one digit. We transfer:

After moving the decimal point to the right one digit, the decimal fraction 5.95 became the fraction 59.5. And the decimal fraction 1.7, after moving the decimal point to the right by one digit, turned into the usual number 17. And we already know how to divide a decimal fraction by a regular number. Further calculation is not difficult:

The comma is moved to the right to make division easier. This is allowed because when multiplying or dividing the dividend and the divisor by the same number, the quotient does not change. What does it mean?
This is one of the interesting features of division. It is called the quotient property. Consider expression 9: 3 = 3. If in this expression the dividend and the divisor are multiplied or divided by the same number, then the quotient 3 will not change.
Let's multiply the dividend and divisor by 2 and see what comes out of it:
(9 × 2) : (3 × 2) = 18: 6 = 3
As can be seen from the example, the quotient has not changed.
The same thing happens when we move the comma in the dividend and in the divisor. In the previous example, where we divided 5.91 by 1.7, we moved the comma in the dividend and divisor one digit to the right. After moving the decimal point, the fraction 5.91 was transformed into the fraction 59.1 and the fraction 1.7 was transformed into the usual number 17.
In fact, inside this process there was a multiplication by 10. This is what it looked like:
5.91 × 10 = 59.1
Therefore, the number of digits after the decimal point in the divisor determines what the dividend and divisor will be multiplied by. In other words, the number of digits after the decimal point in the divisor will determine how many digits in the dividend and in the divisor the decimal point will be moved to the right.
Dividing a decimal by 10, 100, or 1000 is done in the same way as . For example, divide 2.1 by 10. Solve this example using a corner:

But there is a second way. It's lighter. The essence of this method is that the comma in the dividend is moved to the left by as many digits as there are zeros in the divisor.
Let's solve the previous example this way. 2.1: 10. We look at the divisor. We are interested in how many zeros there are in it. We see that there is one zero. This means that in the dividend of 2.1 you need to move the decimal point to the left by one digit. We move the comma to the left one digit and see that there are no more digits left. In this case, add another zero before the number. As a result we get 0.21
Let's try to divide 2.1 by 100. There are two zeros in 100. This means that in the dividend 2.1 we need to move the comma to the left by two digits:
2,1: 100 = 0,021
Let's try to divide 2.1 by 1000. There are three zeros in 1000. This means that in the dividend 2.1 you need to move the comma to the left by three digits:
2,1: 1000 = 0,0021
Dividing a decimal fraction by 0.1, 0.01, and 0.001 is done in the same way as . In the dividend and in the divisor, you need to move the decimal point to the right by as many digits as there are after the decimal point in the divisor.
For example, let's divide 6.3 by 0.1. First of all, let’s move the commas in the dividend and divisor to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. This means we move the commas in the dividend and divisor to the right by one digit.
After moving the decimal point to the right one digit, the decimal fraction 6.3 becomes the usual number 63, and the decimal fraction 0.1 after moving the decimal point to the right one digit turns into one. And dividing 63 by 1 is very simple:
This means the value of the expression 6.3: 0.1 is 63
But there is a second way. It's lighter. The essence of this method is that the comma in the dividend is moved to the right by as many digits as there are zeros in the divisor.
Let's solve the previous example this way. 6.3: 0.1. Let's look at the divisor. We are interested in how many zeros there are in it. We see that there is one zero. This means that in the dividend of 6.3 you need to move the decimal point to the right by one digit. Move the comma to the right one digit and get 63
Let's try to divide 6.3 by 0.01. The divisor of 0.01 has two zeros. This means that in the dividend 6.3 we need to move the decimal point to the right by two digits. But in the dividend there is only one digit after the decimal point. In this case, you need to add another zero at the end. As a result we get 630
Let's try to divide 6.3 by 0.001. The divisor of 0.001 has three zeros. This means that in the dividend 6.3 we need to move the decimal point to the right by three digits:
6,3: 0,001 = 6300
Did you like the lesson?
Join our new VKontakte group and start receiving notifications about new lessons
A lesson-game on the topic: “Actions on decimal fractions” is carried out in the form of a “mathematical train”
Purpose: to test knowledge of the rules of addition, subtraction, multiplication and division with decimal fractions, the ability to apply them in action (in examples, problems).
“The Mathematical Train” consists of three carriages: soft, compartment, reserved seat.
Rules for obtaining a travel ticket.
"Cashroom"
Each student receives a boarding pass with assignments and six tokens.
1. Having solved all the tasks, the student applies for a ticket.
2. If a student cannot solve any task, he turns to the help desk for help. Depending on the content of the certificate, the “fee” is determined.
"Inquiry Office".
1. Checking the correctness of the solution to the task and indicating the error is free of charge.
2. For a leading question that helps you find a way to solve a task, you should pay 1 token.
3. Fee for hinting a solution - 2 tokens.
4. Solution fee – 3 tokens.
“Conditions for obtaining a ticket.”
1. A ticket for a soft carriage is issued upon correct completion of all tasks and presentation of more than 3 tokens to the ticket office.
2. Correct solution of all problems and the presence of three tokens gives the right to receive a ticket to the compartment carriage.
3. One or two tokens are enough for a reserved seat carriage if all tasks are solved correctly.
During the classes.
"Cashroom"
Warm-up
1. Let us recall the rules for adding and subtracting decimal fractions.
Orally (at the board). In writing (on a piece of paper).
3. Let us remember the rule of dividing by a decimal fraction.
Orally (at the board) Written (on pieces of paper).
After verification, “boarding tickets” are issued: a yellow flag for a soft carriage, a green flag for a compartment carriage, a red flag for a reserved seat.
Attention! Attention! The train “Decimals” departs from the station “ Gymnasium" to the station Decide.” The announcer's voice about the train's departure from the station and its arrival at the station should be recorded on a tape recorder. This small touch improvises reality, gives the lesson seriousness and arouses interest.
Smart guys, true friends!”
Our train arrives at the Decide-ka station. You are greeted by the candidate of economic sciences “Arithmetic mean.”
1. How to find the arithmetic mean of several numbers?
2. How to find the average speed?
3. How to find the average price of a product?
4. How to find average daily earnings?
5. How to find the average yield?
(overhead projector)
1. In the volleyball team, 2 players are 21 years old, 3 players are 20 years old, 1 player is 24 years old.
What average age team players? Answer: 21 years old.
2. Weight of 4 chickens – 5.5 kg, 6 chickens – 7.4 kg. Calculate average weight chicken. Answer: 1.29 kg.
3. The first number is 3 times less than the second number. The arithmetic mean of these numbers is 12. Find these numbers. Answer: 6 and 18.
Independent work.
1. Find the arithmetic mean of the numbers 23.86; 22.7; 36.6. Answer: 27.72.
2. The boat covered 22.7 km in 2 hours and covered 42.8 km in 3 hours. Determine the average speed. Answer: 13.1 km.
3. The arithmetic mean of two numbers is 0.48. One of them is 1.4 times larger than the other. Find these numbers. Answer: 0.4 and 0.56.
(Checking solutions through an overhead projector).
The train departs to the Vesna station.
Problem (the condition is written on the board). Finding a solution with a class.
Two starlings simultaneously flew out of one birdhouse in opposite directions. After 0.15 hours there were 16.5 km between them. The flight speed of one starling is 52.4 km/h. Find the other's flight speed.
Independent problem solving.
Two bees simultaneously flew out from one hive in opposite directions. After 0.15 hours there were 6.3 km between them. One flew at a speed of 21.6 km/h. Find the flight speed of the other bee. Answer: 20.4 km/h.
Examination. Two students solve the problem from the back of the board: one using the arithmetic method, the other using the algebraic method.
“Guess” station.
At this station the guys are met by Dunno. Help Dunno quickly correct funny inequalities (put commas in the right place).
42 + 17 = 212 Correct solution: 4.2 +17 = 21.2
3 + 108 = 408 3 + 1,08 = 4,08
57 – 4 = 17 5,7 – 4 = 1,7.
Announcer: “There are inspectors working in the carriages, present the colored cards you received for correctly solving tasks during the trip. Our train is returning to the station.” Gymnasium”!
Total number of colored cards. What did we repeat?
The journey is over.
Sandakova N.A.
Place of work, position:
Teacher of physics and mathematics MBOU "Secondary school named after V.S. Arkhipov, Semenovka village, Yoshkar-Ola"
Mari El Republic
Characteristics of the lesson (lesson)
The level of education:
Basic general education
The target audience:
Teacher (teacher)
Class(es):
Item(s):
Mathematics
The purpose of the lesson:
Systematization of knowledge on the topic “Actions with decimals”: addition, subtraction, multiplication, division of decimals.
Developing the ability to find errors in examples, analyze examples and problems.
Development logical thinking, sociability, sense of teamwork, ability to evaluate one’s knowledge and skills.
Lesson type:
Lesson on generalization and systematization of knowledge
Students in the class (auditorium):
Textbooks used and teaching aids:
Mathematics 5th grade. Vilenkin.
Short description:
A lesson using a computer presentation to review and summarize operations with decimals. Particular attention is paid to the ability to find and correct errors in examples, analyze solutions on the board, and evaluate your knowledge on the topics being studied.
Lesson topic: Those extraordinary decimals.
Goals:
Educational - generalization and systematization of students’ knowledge on the topic “Actions with decimals.”
Developmental - development of students’ logical thinking, cognitive activity, development of independence, ability to self-control, self-esteem.
Educational - nurturing a sense of collectivism, responsibility, and interest in the subject.
Formation of UUD: communicative, cognitive, regulatory.
Lesson type: lesson of generalization and systematization of students’ knowledge and skills.
Form of organization: travel lesson.
Equipment: multimedia computer, presentation.
Handout: stars of different colors (red-5, yellow-4, blue-3) for self-esteem.
Lesson motto: “Flight is mathematics” (V. Chkalov)
During the classes
1. Organizing time.
Let's remember what we studied in fifth grade (slide 2): ordinary and decimal fractions, addition and subtraction, multiplication and division of fractions, comparison, finding fractions from a number, percentages. What is the importance of studying mathematics. The following poem tells us about this.
The teacher reads a poem:
The rocket crossed the sky
Her journey into space is not new for a long time.
You can't hear the rumble and hum
Already from under the cloudy carpets.
And the tamed peaceful atom
Obedient to the reason of people;
Above Padun, compressed by a dam -
Light of electric lights!
All this is the fruit of human searches,
All this was not created suddenly
The mighty power of accurate knowledge
And the skill of the workers!
And before that, please note by the way.
That rocket was given a sight,
Her route is a mathematician
Flew on the wings of formulas.
Dry lines of equations,
The power of reason flowed into them,
They contain an explanation of phenomena,
Things unraveled connection!
Without mathematics there would not be many things that we are used to using.
V. Chkalov said: “Flight is mathematics.” And indeed, the conquest of space was not without mathematical calculations.
Today we also have to make a space journey from the mathematics classroom to various planets of our “School Galaxy”. We will travel by ship.....
You can guess the name of the ship if you arrange the numbers in ascending order: 0.81(n), 1.81(r), 0.081(e), 3.51(i), 3.15(i), 2.44(r) , 0.82(e).
Task on the board. Frontal work with the class.
Answer: Energy.
Teacher: So, we are setting off on a flight on the Energia ship.
The purpose of our flight: to show our guests what knowledge and skills you have acquired on the topic “Decimal Fractions”. During the flight, you need to make your own “star” map (Everyone learns a set of stars of three colors: red-5, yellow-4, blue-3). Self-assessment of knowledge or assessment of the answer by the teacher is carried out.
The rocket is at the start. But before we go on a trip, we need to prepare for the flight.
Preparing for the flight:
1. Repetition of theoretical knowledge:
The teacher begins the sentence, the students continue (do not repeat after the teacher)…
1. To add two decimals...
2. To subtract another from one decimal fraction...
3. To multiply a decimal fraction by 10,...
4. To multiply a decimal fraction by 0.01….
5. To multiply a decimal fraction by a decimal fraction,...
6. To divide a decimal fraction by a decimal fraction,...
7. To find the arithmetic mean of two or more numbers,...
Teacher: Conduct a self-assessment of your knowledge and stick a star on your star map.
2. Verbal counting(on the cards there are tasks for all actions with decimals).
Teacher: Conduct a self-assessment of your knowledge and put a star on it.
Planet "Mathematical"
Teacher: The first planet we arrived on was “Mathematical”. You need to show how you can apply the rules you have learned to calculations. The first example goes to the board to solve..., the second example at the board solves.... We write down the third example in a notebook and solve it ourselves.
1) 296.2 - 2.7 * 6.6: 0.15 Answer: 318.38.
2) 135.2 * 2.1 - (0.083 + 0.841) : 2.31. Answer: 283, 52.
3) 2.575: 2.5 - 4.25 * 0.16 + 0.03 Answer: 0.38.
We are checking the solution. Look at the slide and find your example answers. Whoever gets it right gets a star.
Planet "Historical"
Teacher: Let's continue the flight. Our rocket ended up on the “Historical” planet.
Students prepared reports on the history of the origin of decimal fractions at home. Self-assessment of your performances is an asterisk.
1st student: Decimal fractions were first used by the remarkable Uzbek scientist al-Kashi. At the beginning of the 15th century. In Central Asia, a large observatory was created near the city of Samarkand. It made observations of the movements of stars, planets and the Sun, calculated days of holidays, etc. The best scientists of that time worked at the observatory. The observatory was headed by the scientist Jemshid ib-Masud al-Kashi.
2nd student: In 1427, al-Kashi finished the book “The Key to Arithmetic.” In this book, for the first time in the world, he used decimal fractions, gave rules for operating with them, explained these rules with examples, and described in detail the new system he discovered for writing fractions. To designate categories, he used different options: he separated them with a vertical line, wrote them in different inks, and sometimes wrote out the name of the category completely in words.
Planet "Cognitive".
Teacher: The next planet visited by our rocket is “Cognitive”.
Let's find out the answers to the equations and solve the word. The first and second equations are solved at the board... The third and fourth are decided locally.
Solve equations: (solving equations for testing - behind a closed board)
1) 9x + 3.9 = 31.8 2) (y + 4.5): 7 = 1.2. 3) (y - 8.48) + 2.16 = 3.9
x = 3.1. y = 3.9. y = 10.22.
4) 4y + 7y + 1.8 = 9.5
Answer: plus. Checking answers, finding answers in the table and guessing the word.. Self-assessment: those who solved it correctly receive stars.
Planet "Entertaining".
Teacher: The next planet is “Entertaining.”
Here you will find tasks of an unusual nature. The tasks are written on the board. Frontal work with the class.
1. In which example was the mistake made? Explain.
A) 3.7 + 1.2 = 4.9_B) 7.34 + 10.1 = 17.35
C) 4.2 - 2.03 = 2.17_D) 8.95 - 0.6 = 8.89
2. Place commas to form correct equalities:
1) 42 + 17 = 212 3) 57 - 4 = 17 2) 63 - 27 = 603
3. Enter the action signs:
a) 8.8 10 = 88; b) 3.3 100 = 0.033; c) 7.5 100 = 750.
4. Write down the missing number:
A) 42, 3 * = 423; b) 0.05 * = 50; c) 3800 * = 380.
Self-esteem.
Planet "Creative".
Teacher: The next planet we arrived on is “Creative”.
Based on the drawing, you have to create a text problem for movement and solve it: (solution with commentary). The drawing is made on a poster. View various ways solutions to this problem.
Rice: 15.4 km/h
km/h, 4 times >
In 3 hours Will it catch up in? h.
Teacher's assessment of the answer.
Planet "Theatrical".
Teacher: Our ship arrived on the planet “Teatralnaya”. The aliens invited you to perform a concert program and the jury rated your performance with the following ratings (grades are posted on the board): 4.2; 4.8; 5.0; 4.6; 4.3; 4.7; 4.9.
Find the arithmetic mean and round the result to tenths. Answer: 4.6. Self-esteem.
Planet "Finish".
The last planet is “Finish”. Summing up the lesson.
Now let's see what kind of star card we got, who got how many stars. Let's self-assess our knowledge. Look at the slide: I read a statement to you, and you raise your hand if you agree.
I can multiply fractions.
I can divide a fraction by another fraction.
I can solve equations.
Learned to find the percentage of a number.
I'm learning to solve problems.
Basically everyone learned. It’s only more difficult for you and me when solving problems. Thank you. Well done. We submit notebooks with class work and our own stars for checking.
D/z: Compose a fairy tale on the topic: “Journey to the land of decimals.”