From 11 all operations with fractions. Actions with fractions. Examples of multiplying fractions with variables

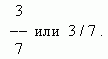
1. The rule for adding fractions with the same denominators:

Example 1:

Example 2:

Rule for adding fractions with different denominators:

Example 1:

Example 2:

Here the denominators were not multiplied, but the least common factor a2 was taken.
(The denominator has the highest power of 2.)
An additional factor for the first fraction is 1, for the second it is a.

2. Rule for subtracting fractions with like denominators:

Rule for subtracting fractions with different denominators:

3. Rule for multiplying ordinary fractions:

4. Rule for dividing fractions:

Example:

Ordinary (simple) fraction. Numerator and denominator of a fraction.
Proper and improper fractions. Mixed number.
Incomplete quotient. Integer and fractional parts. Reverse fractions. Part of a unit or several parts of it are called ordinary or simple fraction. The number of equal parts into which the unit is divided is called the denominator, and the number of parts taken is called the numerator. The fraction is written as:

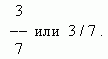
Here 3 is the numerator, 7 is the denominator.

If the numerator is less than the denominator, then the fraction is less than 1 and is called proper fraction. If the numerator is equal to the denominator, then the fraction is equal to 1. If the numerator is greater than the denominator, then the fraction is greater than 1. In both of the latter cases, the fraction is called improper. If the numerator is divided by the denominator, then this fraction is equal to the quotient of the division: 63 / 7 = 9. If the division is performed with a remainder, then this improper fraction can be represented mixed number:

Here 9 – incomplete quotient(integer part of a mixed number), 2 – remainder (numerator of the fractional part), 7 – denominator.
It is often necessary to solve the inverse problem - reverse a mixed number into a fraction. To do this, multiply the integer part of the mixed number by the denominator and add the numerator of the fractional part. This will be the numerator of the common fraction, but the denominator remains the same.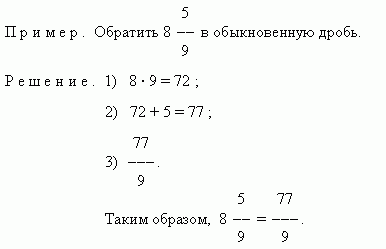

Reciprocal fractions are two fractions whose product is equal to 1. For example, 3 / 7 and 7 / 3; 15/1 and 1/15, etc.

Fraction expansion. Reducing a fraction. Comparing fractions.
Reduction to a common denominator. Addition and subtraction fractions.
Multiplying fractions. Division of fractions
Fraction expansion.The value of a fraction does not change if its numerator and denominator are multiplied by the same number other than zero by expanding the fraction. For example,

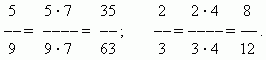
Reducing a fraction. The value of a fraction does not change if you divide its numerator and denominator by the same number other than zero.. This transformation is calledreducing a fraction. For example,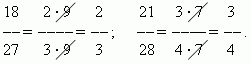

Comparing fractions.Of two fractions with the same numerators, the one whose denominator is smaller is greater:

Of two fractions with the same denominator, the one whose numerator is greater is greater:

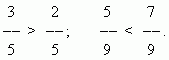
To compare fractions that have different numerators and denominators, you need to expand them to bring them to a common denominator.
EXAMPLE Compare two fractions:

The transformation used here is called bringing fractions to a common denominator.
Adding and subtracting fractions.If the denominators of the fractions are the same, then in order to add the fractions, you need to add their numerators, and in order to subtract the fractions, you need to subtract their numerators (in the same order). The resulting sum or difference will be the numerator of the result; the denominator will remain the same. If the denominators of the fractions are different, you must first reduce the fractions to a common denominator. When adding mixed numbers, their whole and fractional parts are added separately. When subtracting mixed numbers, we recommend first converting them to improper fractions, then subtracting one from the other, and then converting the result again, if necessary, to mixed number form.
EXAMPLE

Multiplying fractions.To multiply a number by a fraction means to multiply it by the numerator and divide the product by the denominator. Therefore, we have a general rule for multiplying fractions:to multiply fractions, you need to multiply their numerators and denominators separately and divide the first product by the second.
EXAMPLE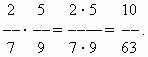
Dividing fractions. In order to divide a certain number by a fraction, it is necessary to multiply this number by the reciprocal fraction. This rule follows from the definition of division (see the section “Arithmetic operations”).
EXAMPLE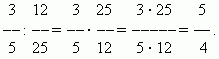

Decimal. The whole part. Decimal point.
Decimal places. Properties of decimal fractions.
Periodic decimal fraction. Period
Decimalis the result of dividing one by ten, one hundred, thousand, etc. parts. These fractions are very convenient for calculations, since they are based on the same positional system on which counting and writing integers are based. Thanks to this, the notation and rules for working with decimal fractions are essentially the same as for whole numbers. When writing decimal fractions, there is no need to mark the denominator; this is determined by the place occupied by the corresponding digit. First it is written whole part numbers, then put on the rightdecimal point. The first digit after the decimal point means the number of tenths, the second – the number of hundredths, the third – the number of thousandths, etc. The numbers located after the decimal point are calleddecimals.
EXAMPLE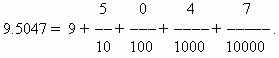
One of the advantages of decimal fractions is that they are easily reduced to ordinary fractions: the number after the decimal point (in our case 5047) is the numerator; the denominator is equal n -th power of 10, where n - number of decimal places (in our case n = 4):
If the decimal fraction does not contain an integer part, then a zero is placed before the decimal point:

Properties of decimal fractions.

1. The decimal does not change if you add zeros to the right:

2. The decimal fraction does not change if you remove the zeros located
at the end of the decimal:

0.00123000 = 0.00123 .

Attention! You cannot remove zeros that are not located at the end decimal!br />

These properties allow you to quickly multiply and divide decimals by 10, 100, 1000, etc.

Periodic decimal contains an infinitely repeating group of numbers called a period. The period is written in brackets. For example, 0.12345123451234512345… = 0.(12345).

EXAMPLE If we divide 47 by 11, we get 4.27272727... = 4.(27).

Multiplying decimals.
Dividing decimals.

Adding and subtracting decimals. These operations are performed in the same way as adding and subtracting integers. You just need to write down the corresponding decimal places one below the other.
EXAMPLE

Multiplying decimals. At the first stage, we multiply decimal fractions as whole numbers, without taking into account the decimal point. Then the following rule applies: the number of decimal places in the product is equal to the sum of the decimal places in all factors.
Note: before placing the decimal point inthe product cannot be discarded with trailing zeros!
EXAMPLE

The sum of the numbers of decimal places in the factors is equal to: 3 + 4 = 7. The sum of the numbers in the product is 6. Therefore, you need to add one zero to the left: 0197056 and put a decimal point in front of it: 0.0197056.
Decimal division
Dividing a decimal by a whole number
If dividend is less than divisor, write a zero in the integer part of the quotient and put a decimal point after it. Then, without taking into account the decimal point of the dividend, we add the next digit of the fractional part to its integer part and again compare the resulting integer part of the dividend with the divisor. If the new number is again less than the divisor, we put another zero after the decimal point in the quotient and add the next digit of its fractional part to the whole part of the dividend. We repeat this process until the resulting dividend becomes greater than the divisor. After this, division is performed as for integers. If the dividend is greater than or equal to the divisor, first we divide its whole part, write the result of division in the quotient and put a decimal point. After this, division continues as in the case of integers.
EXAMPLE Divide 1.328 by 64.
Solution: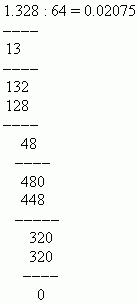
Dividing one decimal fraction by another.
First, we transfer the decimal points in the dividend and divisor to the number of decimal places in the divisor, that is, we make the divisor an integer. Now we perform division as in the previous case.
EXAMPLE Divide 0.04569 by 0.0006.
Solution: Move the decimal points 4 positions to the right and divide 456.9 by 6:

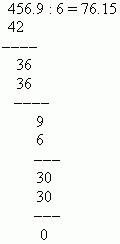
In order to convert a decimal fraction into an ordinary fraction, you need to take the number after the decimal point as the numerator, and take the nth power of ten as the denominator (here n is the number of decimal places). The non-zero integer part is stored in an ordinary fraction; the zero integer part is omitted. For example:
In order to convert a fraction to a decimal, you must divide the numerator by the denominator in accordance with the division rules.
EXAMPLE Convert 5/8 to a decimal.
Solution: Dividing 5 by 8 gives 0.625. (Check, please!).
In most cases, this process can continue indefinitely. Then it is impossible to accurately convert a fraction to a decimal. But in practice this is never required. The division is aborted if the decimal places of interest have already been obtained.
EXAMPLE Convert 1/3 to a decimal.
Solution: Dividing 1 by 3 will be infinite: 1:3 = 0.3333… .
Check it out please!

This section covers operations with ordinary fractions. If it is necessary to carry out a mathematical operation with mixed numbers, then it is enough to convert the mixed fraction into an extraordinary fraction, carry out the necessary operations and, if necessary, present the final result again in the form of a mixed number. This operation will be described below.

Reducing a fraction

Mathematical operation. Reducing a fraction

To reduce the fraction \frac(m)(n) you need to find the greatest common divisor of its numerator and denominator: gcd(m,n), and then divide the numerator and denominator of the fraction by this number. If GCD(m,n)=1, then the fraction cannot be reduced. Example: \frac(20)(80)=\frac(20:20)(80:20)=\frac(1)(4)

Usually, immediately finding the greatest common divisor seems to be a difficult task, and in practice, a fraction is reduced in several stages, step by step isolating obvious common factors from the numerator and denominator. \frac(140)(315)=\frac(28\cdot5)(63\cdot5)=\frac(4\cdot7\cdot5)(9\cdot7\cdot5)=\frac(4)(9)

Reducing fractions to a common denominator

Mathematical operation. Reducing fractions to a common denominator

To bring two fractions \frac(a)(b) and \frac(c)(d) to a common denominator you need:

• find the least common multiple of the denominators: M=LMK(b,d);
• multiply the numerator and denominator of the first fraction by M/b (after which the denominator of the fraction becomes equal to the number M);
• multiply the numerator and denominator of the second fraction by M/d (after which the denominator of the fraction becomes equal to the number M).

Thus, we transform the original fractions to fractions with the same denominators (which will be equal to the number M).

For example, the fractions \frac(5)(6) and \frac(4)(9) have LCM(6,9) = 18. Then: \frac(5)(6)=\frac(5\cdot3)(6 \cdot3)=\frac(15)(18);\quad\frac(4)(9)=\frac(4\cdot2)(9\cdot2)=\frac(8)(18) . Thus, the resulting fractions have a common denominator.

In practice, finding the least common multiple (LCM) of denominators is not always a simple task. Therefore, a number equal to the product of the denominators of the original fractions is chosen as the common denominator. For example, the fractions \frac(5)(6) and \frac(4)(9) are reduced to a common denominator N=6\cdot9:

\frac(5)(6)=\frac(5\cdot9)(6\cdot9)=\frac(45)(54);\quad\frac(4)(9)=\frac(4\cdot6)( 9\cdot6)=\frac(24)(54)

Comparison of fractions

Mathematical operation. Comparison of fractions

To compare two ordinary fractions you need:

• compare the numerators of the resulting fractions; a fraction with a larger numerator will be larger.

When comparing fractions, there are several special cases:

1. From two fractions with the same denominators The fraction whose numerator is greater is greater. For example, \frac(3)(15)
2. From two fractions with the same numerators The larger is the fraction whose denominator is smaller. For example, \frac(4)(11)>\frac(4)(13)
3. That fraction which simultaneously larger numerator and smaller denominator, more. For example, \frac(11)(3)>\frac(10)(8)

Attention! Rule 1 applies to any fractions if their common denominator is a positive number. Rules 2 and 3 apply to positive fractions (those with both the numerator and denominator greater than zero).

Adding and subtracting fractions

Mathematical operation. Adding and subtracting fractions

To add two fractions you need:

• bring them to a common denominator;
• add their numerators and leave the denominator unchanged.

Example: \frac(7)(9)+\frac(4)(7)=\frac(7\cdot7)(9\cdot7)+\frac(4\cdot9)(7\cdot9)=\frac(49 )(63)+\frac(36)(63)=\frac(49+36)(63)=\frac(85)(63)

To subtract another from one fraction, you need:

• reduce fractions to a common denominator;
• Subtract the numerator of the second fraction from the numerator of the first fraction and leave the denominator unchanged.

Example: \frac(4)(15)-\frac(3)(5)=\frac(4)(15)-\frac(3\cdot3)(5\cdot3)=\frac(4)(15) -\frac(9)(15)=\frac(4-9)(15)=\frac(-5)(15)=-\frac(5)(3\cdot5)=-\frac(1)( 3)

If the original fractions initially have a common denominator, then step 1 (reduction to a common denominator) is skipped.

Converting a mixed number to an improper fraction and vice versa

Mathematical operation. Converting a mixed number to an improper fraction and vice versa

To convert a mixed fraction to an improper fraction, simply sum the whole part of the mixed fraction with the fraction part. The result of such a sum will be an improper fraction, the numerator of which is equal to the sum of the product of the whole part by the denominator of the fraction with the numerator of the mixed fraction, and the denominator will remain the same. For example, 2\frac(6)(11)=2+\frac(6)(11)=\frac(2\cdot11)(11)+\frac(6)(11)=\frac(2\cdot11+ 6)(11)=\frac(28)(11)

To convert an improper fraction to a mixed number:

• divide the numerator of a fraction by its denominator;
• write the remainder of the division into the numerator and leave the denominator the same;
• write the result of the division as an integer part.

For example, the fraction \frac(23)(4) . When dividing 23:4=5.75, that is, the whole part is 5, the remainder of the division is 23-5*4=3. Then the mixed number will be written: 5\frac(3)(4) . \frac(23)(4)=\frac(5\cdot4+3)(4)=5\frac(3)(4)

Converting a Decimal to a Fraction

Mathematical operation. Converting a Decimal to a Fraction

In order to convert a decimal fraction to a common fraction, you need to:

1. take the nth power of ten as the denominator (here n is the number of decimal places);
2. as the numerator, take the number after the decimal point (if the integer part of the original number is not equal to zero, then take all the leading zeros as well);
3. the non-zero integer part is written in the numerator at the very beginning; the zero integer part is omitted.

Example 1: 0.0089=\frac(89)(10000) (there are 4 decimal places, so the denominator has 10 4 =10000, since the integer part is 0, the numerator contains the number after the decimal point without leading zeros)

Example 2: 31.0109=\frac(310109)(10000) (in the numerator we write the number after the decimal point with all zeros: “0109”, and then before it we add the whole part of the original number “31”)

If the whole part of a decimal fraction is non-zero, then it can be converted to a mixed fraction. To do this, we convert the number into an ordinary fraction as if the whole part were equal to zero (points 1 and 2), and simply rewrite the whole part in front of the fraction - this will be the whole part of the mixed number. Example:

3.014=3\frac(14)(100)

To convert a fraction to a decimal, simply divide the numerator by the denominator. Sometimes you end up with an infinite decimal. In this case, it is necessary to round to the desired decimal place. Examples:

\frac(401)(5)=80.2;\quad \frac(2)(3)\approx0.6667

Multiplying and dividing fractions

Mathematical operation. Multiplying and dividing fractions

To multiply two ordinary fractions, you need to multiply the numerators and denominators of the fractions.

\frac(5)(9)\cdot\frac(7)(2)=\frac(5\cdot7)(9\cdot2)=\frac(35)(18)

To divide one common fraction by another, you need to multiply the first fraction by the reciprocal of the second ( reciprocal fraction- a fraction in which the numerator and denominator are swapped.

\frac(5)(9):\frac(7)(2)=\frac(5)(9)\cdot\frac(2)(7)=\frac(5\cdot2)(9\cdot7)= \frac(10)(63)

If one of the fractions is a natural number, then the above rules of multiplication and division remain in force. You just need to take into account that an integer is the same fraction, the denominator of which is equal to one. For example: 3:\frac(3)(7)=\frac(3)(1):\frac(3)(7)=\frac(3)(1)\cdot\frac(7)(3)= \frac(3\cdot7)(1\cdot3)=\frac(7)(1)=7

1º. Integers- These are numbers used in counting. The set of all natural numbers is denoted by N, i.e. N=(1, 2, 3, …).

Fraction is a number consisting of several fractions of a unit. Common fraction is a number of the form where is a natural number n shows how many equal parts a unit is divided into, and a natural number m shows how many such equal parts are taken. Numbers m And n are called accordingly numerator And denominator fractions

If the numerator is less than the denominator, then the fraction is called correct; if the numerator is equal to or greater than the denominator, then the fraction is called wrong. A number consisting of an integer and a fractional part is called mixed number.

For example,
- proper ordinary fractions,
- improper ordinary fractions, 1 is a mixed number.

2º. When performing operations with ordinary fractions, you should remember the following rules:

1)The main property of a fraction. If the numerator and denominator of a fraction are multiplied or divided by the same natural number, you get a fraction equal to the given one.

For example, a)
; b)
.

Dividing the numerator and denominator of a fraction by their common divisor other than one is called reducing a fraction.

2) To represent a mixed number as an improper fraction, you need to multiply its whole part by the denominator of the fractional part and add the numerator of the fractional part to the resulting product, write the resulting amount as the numerator of the fraction, and leave the denominator the same.

Similarly, any natural number can be written as an improper fraction with any denominator.

For example, a)
, because
; b)
etc.

3) To write an improper fraction as a mixed number (i.e., separate an integer part from an improper fraction), you need to divide the numerator by the denominator, take the quotient of the division as an integer part, the remainder as the numerator, and leave the denominator the same.

For example, a)
, since 200: 7 = 28 (remaining 4); b)
, since 20: 5 = 4 (remaining 0).

4) To reduce fractions to the lowest common denominator, you need to find the least common multiple (LCM) of the denominators of these fractions (it will be their lowest common denominator), divide the lowest common denominator by the denominators of these fractions (i.e. find additional factors for the fractions) , multiply the numerator and denominator of each fraction by its additional factor.

For example, let's give the fractions
to the lowest common denominator:

,
,
;

630: 18 = 35, 630: 10 = 63, 630: 21 = 30.

Means,
;
;
.

5) Rules for arithmetic operations on ordinary fractions:

a) Addition and subtraction of fractions with the same denominators is performed according to the rule:

.

b) Addition and subtraction of fractions with different denominators is carried out according to rule a), after first reducing the fractions to the lowest common denominator.

c) When adding and subtracting mixed numbers, you can turn them into improper fractions, and then follow the rules a) and b),

d) When multiplying fractions, use the following rule:

.

e) To divide one fraction by another, you need to multiply the dividend by the reciprocal of the divisor:

.

f) When multiplying and dividing mixed numbers, they are first converted to improper fractions, and then rules d) and e) are used.

3º. When solving examples for all operations with fractions, remember that the operations in parentheses are performed first. Both inside and outside parentheses, multiplication and division are performed first, followed by addition and subtraction.

Let's look at the implementation of the above rules using an example.

Example 1. Calculate:
.

1)
;

2)
;

5)
. Answer: 3.

Actions with fractions. In this article we will look at examples, everything in detail with explanations. We will consider ordinary fractions. We'll look at decimals later. I recommend watching the whole thing and studying it sequentially.

1. Sum of fractions, difference of fractions.

Rule: when adding fractions with equal denominators, the result is a fraction - the denominator of which remains the same, and its numerator will be equal to the sum of the numerators of the fractions.

Rule: when calculating the difference between fractions with the same denominators, we obtain a fraction - the denominator remains the same, and the numerator of the second is subtracted from the numerator of the first fraction.

Formal notation for the sum and difference of fractions with equal denominators:

Examples (1):

It is clear that when ordinary fractions are given, then everything is simple, but what if they are mixed? Nothing complicated...

Option 1– you can convert them into ordinary ones and then calculate them.

Option 2– you can “work” separately with the integer and fractional parts.

Examples (2):

More:

What if the difference of two mixed fractions is given and the numerator of the first fraction is less than the numerator of the second? You can also act in two ways.

Examples (3):

*Converted to ordinary fractions, calculated the difference, converted the resulting improper fraction to a mixed fraction.

*We broke it down into integer and fractional parts, got a three, then presented 3 as the sum of 2 and 1, with one represented as 11/11, then found the difference between 11/11 and 7/11 and calculated the result. The meaning of the above transformations is to take (select) a unit and present it in the form of a fraction with the denominator we need, then we can subtract another from this fraction.

Another example:

Conclusion: there is a universal approach - in order to calculate the sum (difference) of mixed fractions with equal denominators, they can always be converted to improper ones, then perform the necessary action. After this, if the result is an improper fraction, we convert it to a mixed fraction.

Above we looked at examples with fractions that have equal denominators. What if the denominators are different? In this case, the fractions are reduced to the same denominator and the specified action is performed. To change (transform) a fraction, the basic property of the fraction is used.

Let's look at simple examples:

In these examples, we immediately see how one of the fractions can be transformed to get equal denominators.

If we designate ways to reduce fractions to the same denominator, then we will call this one METHOD ONE.

That is, immediately when “evaluating” a fraction, you need to figure out whether this approach will work - we check whether the larger denominator is divisible by the smaller one. And if it is divisible, then we perform a transformation - we multiply the numerator and denominator so that the denominators of both fractions become equal.

Now look at these examples:

This approach is not applicable to them. There are also ways to reduce fractions to a common denominator; let’s consider them.

Method TWO.

We multiply the numerator and denominator of the first fraction by the denominator of the second, and the numerator and denominator of the second fraction by the denominator of the first:

*In fact, we reduce fractions to form when the denominators become equal. Next, we use the rule for adding fractions with equal denominators.

Example:

*This method can be called universal, and it always works. The only downside is that after the calculations you may end up with a fraction that will need to be further reduced.

Let's look at an example:

It can be seen that the numerator and denominator are divisible by 5:

Method THREE.

You need to find the least common multiple (LCM) of the denominators. This will be the common denominator. What kind of number is this? This is the smallest natural number that is divisible by each of the numbers.

Look, here are two numbers: 3 and 4, there are many numbers that are divisible by them - these are 12, 24, 36, ... The smallest of them is 12. Or 6 and 15, they are divisible by 30, 60, 90 .... The least is 30. The question is - how to determine this least common multiple?

There is a clear algorithm, but often this can be done immediately without calculations. For example, according to the above examples (3 and 4, 6 and 15) no algorithm is needed, we took large numbers (4 and 15), doubled them and saw that they are divisible by the second number, but pairs of numbers can be others, for example 51 and 119.

Algorithm. In order to determine the least common multiple of several numbers, you must:

- decompose each number into SIMPLE factors

— write down the decomposition of the BIGGER of them

- multiply it by the MISSING factors of other numbers

Let's look at examples:

50 and 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5

in the expansion of a larger number one five is missing

=> LCM(50,60) = 2∙2∙3∙5∙5 = 300

48 and 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

in the expansion of a larger number two and three are missing

=> LCM(48.72) = 2∙2∙2∙2∙3∙3 = 144

* The least common multiple of two prime numbers is their product

Question! Why is finding the least common multiple useful, since you can use the second method and simply reduce the resulting fraction? Yes, it is possible, but it is not always convenient. Look at the denominator for the numbers 48 and 72 if you simply multiply them 48∙72 = 3456. You will agree that it is more pleasant to work with smaller numbers.

Let's look at examples:

*51 = 3∙17 119 = 7∙17

the expansion of a larger number is missing a triple

=> NOC(51,119) = 3∙7∙17

Now let's use the first method:

*Look at the difference in the calculations, in the first case there are a minimum of them, but in the second you need to work separately on a piece of paper, and even the fraction you received needs to be reduced. Finding the LOC simplifies the work significantly.

More examples:

*In the second example it is clear that the smallest number that is divisible by 40 and 60 is 120.

RESULT! GENERAL COMPUTING ALGORITHM!

— we reduce fractions to ordinary ones if there is an integer part.

- we bring fractions to a common denominator (first we look at whether one denominator is divisible by another; if it is divisible, then we multiply the numerator and denominator of this other fraction; if it is not divisible, we act using the other methods indicated above).

- Having received fractions with equal denominators, we perform operations (addition, subtraction).

- if necessary, we reduce the result.

- if necessary, then select the whole part.

2. Product of fractions.

The rule is simple. When multiplying fractions, their numerators and denominators are multiplied:

Examples: